Rajshahi Board ICT 2024 | Chapter 3 Number System & Logic Gate Solutions | Path Abdur Rahman Prince পাঠ আব্দুর রহমান প্রিন্স

Rajshahi Board ICT 2024

$P=(\text{৩৬)}{)}_{৮}$ এবং $Q=(২F{)}_{১৬}$

ক. কোড কী?
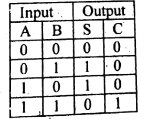
খ. ১১ + ১ = ১০০ হতে পারে- ব্যাখ্যা করো।
গ. P ও Q এর মানকে দশমিক সংখ্যা পদ্ধতিতে প্রকাশ করো।
ঘ. (P - Q) গাণিতিক প্রক্রিয়াটি যোগের মাধ্যমে করা যায়- গাণিতিকভাবে বিশ্লেষণ করো।

$ক$

কোড হলো কোনো বর্ণ, অক্ষর, শব্দ বা চিহ্নকে অদ্বিতীয় হিসেবে বাইনারিতে রূপান্তর করার প্রক্রিয়া।

$খ$

১১ + ১ = ১০০ হতে পারে।

যদি ১১ + ১ এর বাইনারি যোগ করা হয়, তাহলে

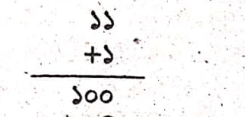
∴ বাইনারি যোগের ক্ষেত্রে ১১ + ১ = ১০০ হওয়া সম্ভব।

$গ$

উদ্দীপকে উল্লিখিত P ও Q এর মানকে দশমিক সংখ্যা পদ্ধতিতে রূপান্তর করা হলো-

$P=(\text{৩৬}{)}_{৮}$

$=৩\times {৮}^{১}+৬\times {৮}^0$

= ২৪+৬

$=(৩০{)}_{১০}$

$Q=(২F{)}_{১৬}$

$=২\times ১{৬}^{১}+১৫\left(F\right)\times ১{৬}^{\circ }$

= ৩২ + ১৫

$=(৪৭{)}_{১০}$

$ঘ$

২'এর পরিপূরকের সাহায্যে উদ্দীপকের P-Q গাণিতিক প্রক্রিয়াটি যোগের মাধ্যমে নির্ণয় করা সম্ভব। যোগের মাধ্যমে দুটি সংখ্যার পার্থক্য নির্ণয়ের পদ্ধতির নাম হলো ২'এর পরিপূরক। কোনো বাইনারি সংখ্যার বিটগুলো উল্টিয়ে অর্থাৎ 1-এর স্থলে 0 এবং 0 এর স্থলে 1 দ্বারা প্রতিস্থাপন সংখ্যাটির 1' এর পরিপূরক পাওয়া যায়। আর কোনো বাইনারি সংখ্যার 1' এর পরিপূরকের সাথে 1 যোগ করলে 2' এর পরিপূরক বা 2's Complement পাওয়া যায়।

২' এর পরিপূরকের মূল উদ্দেশ্য হলো কোনো সংখ্যাকে বিপরীতকরণ বা নেগেশন করা। বিপরীতকরণ বা নিগেশনের ফলে কোনো সংখ্যার মানের পরিবর্তন হয় না কিন্তু চিহ্নের পরিবর্তন হয়। তাই ২' এর পরিপূরকের সাহায্যে বিয়োগের কাজ সম্পাদন করা হয় যোগের মাধ্যমে। নিচে ২'এর পরিপূরকের সাহায্যে (P-Q) প্রক্রিয়াটি যোগের মাধ্যমে নির্ণয় করে দেখানো হলো:

দেওয়া আছে-

$P=(36{)}_8=(000111110{)}_2$

এবং

$Q=(2F{)}_{16}=(00101111{)}_2$

সংখ্যা দুটির পার্থক্য,

P-Q

$(00011110{)}_2-{\left({00}^{}101111\right)}_2$

$(00011110{)}_2+(-00101111{)}_2$

এখানে 00101111 ঋণাত্মক। তাই শুধুমাত্র 00101111 এর 2' এর পরিপূরক করতে হবে।

অতএব,

$(-00101111{)}_2=(11010001{)}_2$

সুতরাং,

$P-Q=(00011110{)}_2+(-00101111{)}_2$

$=(00011110{)}_2+(11010001{)}_2$

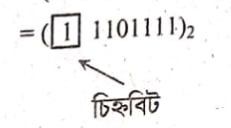
যেহেতু চিহ্নবিট। সেহেতু ফলাফল ঋণাত্মক। অতএব ২'-এর পরিপূরক করে প্রকৃত ফলাফল পাওয়া যাবে।

সুতরাং

∴ নির্ণেয় ফলাফল = -17

Rajshahi Board ICT 2024

ক. সত্যক সারণি কী?
খ. A (A+A) = A ব্যাখ্যা করো।
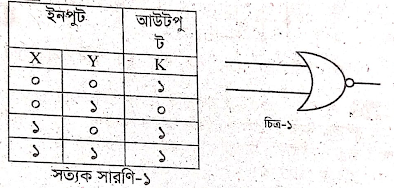
গ. K-এর মান লেখো এবং সরল করো।
ঘ. উদ্দীপকের চিত্র-১ এ নির্দেশিত গেইটটি দিয়ে XOR এর সমতুল্য সার্কিট বাস্তবায়ন করো।

$ক$

যে টেবিল বা সারণির মাধ্যমে বিভিন্ন গেইটের কার্যনীতি প্রকাশ করা হয় তাকে সত্যক সারণি বলে।

$খ$

বুলিয়ান উপপাদ্য ব্যবহার করে যেকোনো ধরনের বুলিয়ান অ্যালজেবরার সমীকরণ নির্ণয় করা যায়।

A(A + A)

= A.A + A.A

=A+A [অপরিবর্তনীয় উপপাদ্য অনুসারে,]

= A [অপরিবর্তনীয় উপপাদ্য অনুসারে, A + A = A]

সুতরাং, A(A + A) = A।

$গ$

উদ্দীপকে সত্যক সারণি-১ হতে প্রাপ্ত K এর মান,

K-এর মান সত্যতা সারণী থেকে নেওয়া যায়:

K = ১, ০, ০, ১।

এটি সারণীর K কলাম থেকে সরাসরি নেওয়া।

$K=\overline{X}\overline{Y}+X\overline{Y}+XY$

নিম্নে K এর মান সরল করা হলো-

$K=\overline{X}\overline{Y}+X\overline{Y}+XY$

$=\overline{Y}(\overline{X}+X)+XY$

$=\overline{Y}+XY[\because \overline{A}+A=1]$

$=(\overline{Y}+X)(\overline{Y}+Y)[\because A+BC=(A+B\left)\right(A+C\left)\right]$

$=(\overline{Y}+X).1$

$=\overline{Y}+X=X+\overline{Y}$

$ঘ$

উদ্দীপকের চিত্র-১ এ নির্দেশিত গেইটটি হলো নর গেইট।

আমরা জানি, XOR গেইটের লজিক ফাংশন,

$X=\overline{A}B+A\overline{B}$

নর গেইট দিয়ে XOR গেইট এর সমতুল্য সার্কিট নিম্নে বাস্তবায়ন করা হলো-

$X=\overline{A}B+A\overline{B}$

$=\overline{\overline{\overline{A}B}}+\overline{\overline{A\overline{B}}}$

$=\overline{\overline{\overline{A}}+\overline{B}}+\overline{\overline{A}+\overline{\overline{B}}}$

$=\overline{A+\overline{B}}+\overline{\overline{A}+B}$

$=\overline{\overline{\overline{A+\overline{B}}+\overline{\overline{A}+B}}}$