Dhaka Board 2024 HSC ICT
ইমন বার্ষিক পরীক্ষার ফলাফল বিশ্লেষণ করতে গিয়ে দেখল বাংলা, ইংরেজি ও ICT বিষয়ে সে যথাক্রমে
নম্বর পেয়েছে।
খ. ১৭ এর পরের সংখ্যাটি ২০ ব্যাখ্যা করো।
গ. উদ্দীপকে ইমনের ইংরেজি বিষয়ে প্রাপ্ত নম্বর হেক্সাডেসিমেলে রূপান্তর করো।
ঘ. উদ্দীপকে ইমনের তিনটি বিষয়ে মোট প্রাপ্ত নম্বর বাইনারিতে কত হবে? নির্ণয় করো।
যে সকল গেইটের সাহায্যে মৌলিক গেইটসহ অন্যান্য সকল প্রকার গেইট তৈরি বা বাস্তবায়ন করা যায় সেই সমস্ত গেইটকে সর্বজনীন বা Universal গেইট বলে।
১৭ এর পরের সংখ্যাটি ২০। এটি প্রমাণ করার জন্য কে প্রথমে ডেসিমেলে রূপান্তর করতে হবে,
= ৮+৭
= ১৫
এখন, ১৫ এর পরবর্তী সংখ্যা ডেসিমেলে,
১৫ + ১ = ১৬
কে অক্টালে রূপান্তর করে পাই,
∴ অক্টাল পদ্ধতিতে ১৭ এর পরের সংখ্যা ২০ হবে।
উদ্দীপকে ইমনের ইংরেজি বিষয়ে প্রাপ্ত নম্বর । ইমনের প্রাপ্ত নম্বরটি অক্টাল হতে ডেসিমেলে রূপান্তর করে পাই,
এখন, কে হেক্সাডেসিমেলে রূপান্তর নিম্নরূপ-
এবং ভাগশেষ থাকে 3।
এবং ভাগশেষ থাকে 5।
এখন, আমরা নিচের দিক থেকে উপরের দিকে ভাগশেষগুলো সাজিয়ে লিখব।
সুতরাং, ইমনের ইংরেজিতে প্রাপ্ত নম্বর হেক্সাডেসিমেলে ।
উদ্দীপকের ইমনের তিনটি বিষয়ে প্রাপ্ত নম্বর,
সুতরাং, ইমনের তিনটি বিষয়ে মোট প্রাপ্ত নম্বর,
Dhaka Board 2024 HSC ICT
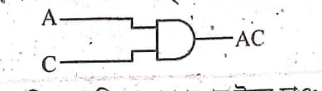
Y = (A+B)
খ. বিয়োগের কাজ যোগের মাধ্যমে করা সম্ভব-ব্যাখ্যা করো।
গ. উদ্দীপকে প্রদত্ত লজিক ফাংশনটির সত্যক সারণি তৈরি করো।
ঘ. "Y কে বুলিয়ান অ্যালজেবরার সাহায্যে সরলীকরণ করার ফলে বর্তনী বাস্তবায়ন সহজ হয়েছে" - বিশ্লেষণপূর্বক উক্তিটির সত্যতা যাচাই করো।
ASCII-এর পূর্ণরূপ হলো- American Standard Code for Information Interchange, যা বহুল প্রচলিত আলফানিউমেরিক কোড।
বিয়োগের কাজ যোগের মাধ্যমে করা সম্ভব ২ এর পরিপূরক পদ্ধতি ব্যবহার করে। বাইনারি সংখ্যার ১ এর পরিপূরকের সাথে ১ যোগ করলে ২ এর পরিপূরক পাওয়া যায়। এক্ষেত্রে যেকোনো ঋণাত্মক সংখ্যার ২ এর পরিপূরক তৈরি করে সমকক্ষ ৮টি বাইনারি সংখ্যার সমান করতে হবে। অতঃপর সংখ্যাদ্বয়ের চূড়ান্ত অবস্থা যোগ করে ফলাফল নির্ণয় করা হয়। তবে চিহ্ন বিট ১ হলে ফলাফল ২ এর পরিপূরক গঠনে থাকে।
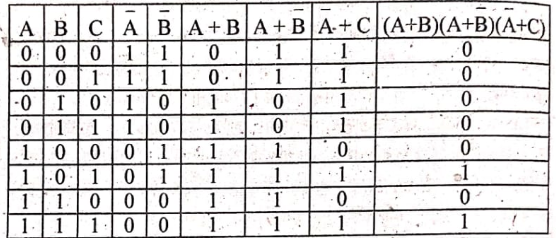
উদ্দীপকে প্রদত্ত লজিক ফাংশনটি হলো,
Y = (A + B)(A + B)(A + C)
লজিক ফাংশনটির সত্যক সারণি নিম্নে দেওয়া হলো-
উদ্দীপকে উল্লিখিত লজিক ফাংশনটি হলো,
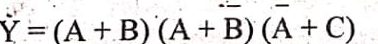
উক্ত ফাংশনের লজিক বর্তনী নিম্নরূপ:
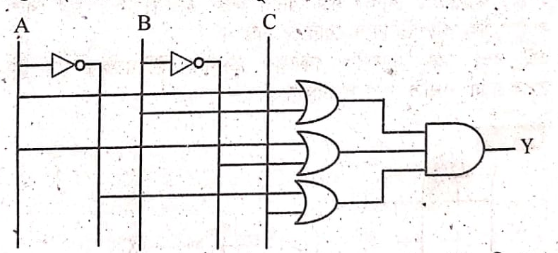
উক্ত ফাংশনের সার্কিট অঙ্কনের জন্য প্রয়োজন হবে নট গেইট ২টি, অর গেইট ৩টি এবং অ্যান্ড গেইট ১টি সহ মোট ৬টি গেইট। এখন, Y কে সরলীকরণ করে পাই,
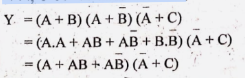
লজিক ফাংশনটি সরলীকরণ করার ফলে ফাংশনটি ছোট আকার ধারণ করেছে। সরলীকরণ করার পূর্বে ফাংশনের আকার বড় হওয়ায় লজিক বর্তনীও বড় ছিল। অতএব, সরল করার ফলে বর্তনীটি ছোট হয়ে এসেছে এবং তা বাস্তবায়ন সহজ হয়েছে। সরলীকৃত ফাংশনটির বর্তনী নিম্নরূপ-