Sylhet Board ICT 2024 | Chapter 3 Number System & Logic Gate Solutions | Path Abdur Rahman Prince পাঠ আব্দুর রহমান প্রিন্স

 Sylhet Board ICT 2024 Question and Solution

  রাশেদ নির্বাচনি পরীক্ষায় বাংলা, ইংরেজি ও আইসিটি বিষয়ে যথাক্রমে $\left(4E{)}_{16n}\right(1011001{)}_2$ ও $(85{)}_{10}$ পেল।

ক. ভিত্তি কী?
খ. বিশ্বের সকল ভাষাকে কোডভুক্ত করা সম্ভব হয়েছে- ব্যাখ্যা করো।
গ. রাশেদের বাংলা ও ইংরেজিতে প্রাপ্ত মোট নম্বর অক্টাল পদ্ধতিতে নির্ণয় করো।
ঘ. উদ্দীপকের আলোকে রাশেদের ইংরেজি ও আইসিটি বিষয়ের প্রাপ্ত নম্বরের পার্থক্য যোগের মাধ্যমে নির্ণয় করা সম্ভব কিনা তা বিশ্লেষণপূর্বক মতামত দাও।

$ক$

কোন সংখ্যা পদ্ধতিকে লিখে প্রকাশ করার জন্য যতগুলো অংক বা সাংকেতিক চিহ্ন ব্যবহৃত হয় তাদের মোট সংখ্যাই হলো সংখ্যা পদ্ধতির ভিত্তিই।

$খ$

বিশ্বের ছোট-বড় সকল ভাষাকে কম্পিউটারের কোডভুক্ত করার জন্য যে কোড ব্যবহৃত হয় তা ইউনিকোড নামে পরিচিত। এটি 2 বাইট বা 16 বিটের কোড যা $2^{16}$ বা 65536 টি চিহ্নকে নির্দিষ্ট করতে পারে। ফলে অনেক দেশের ভাষা এই কোডের মাধ্যমে সহজতর করা সম্ভব হয়েছে।

$গ$

উদ্দীপকে উল্লিখিত রাশেদের বাংলা ও ইংরেজিতে প্রাপ্ত নম্বর যথাক্রমে $(4E{)}_{16}$ ও $(1011001{)}_2$

বাংলায় প্রাপ্ত নম্বর = $(4E{)}_{16}$

$=4\times {16}^1+14\left(E\right)\times {16}^0$

= 64+14

$=(78{)}_{10}$

ইংরেজিতে প্রাপ্ত নম্বর = $(1011001{)}_2$

$=1\times 2^6+0\times 2^5+1\times 2^4+1\times 2^3+0\times 2^2$$+0\times 2^1+1\times 2^0$

=64+16+8+1

$=(89{)}_{10}$

∴ বাংলা ও ইংরেজিতে প্রাপ্ত মোট নম্বর,

$=(78{)}_{10}+(89{)}_{10}=(167{)}_{10}$

বাংলা ও ইংরেজিতে প্রাপ্ত মোট নম্বর অক্টালে রূপান্তর করা হলো,

$\therefore (167{)}_{10}=(247{)}_8$

$ঘ$

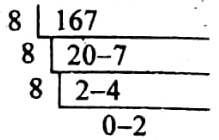
উদ্দীপক অনুযায়ী,

রাশেদের ইংরেজিতে প্রাপ্ত নম্বর $=(1011001{)}_2=(01011001{)}_2$

রাশেদের আইসিটি বিষয়ে প্রাপ্ত নম্বর $=(85{)}_{10}$

$\therefore (85{)}_{10}=(1010101{)}_2=(01010101{)}_2$

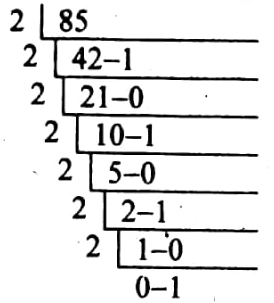
রাশেদের ইংরেজি ও আইসিটি বিষয়ের প্রাপ্ত নম্বরের পার্থক্য যোগের মাধ্যমে অর্থাৎ ২-এর পরিপূরক পদ্ধতিতে নির্ণয় করা সম্ভব। নিম্নে 2- এর পরিপূরক পদ্ধতি ব্যবহার করে ইংরেজি ও আইসিটি বিষয়ে প্রাপ্ত নম্বরের পার্থক্য দেখানো হলো:

ইংরেজি ও আইসিটি বিষয়ে প্রাপ্ত নম্বরের পার্থক্য,

$(01011001{)}_2-(01010101{)}_2$

$=(01011001{)}_2+(-01010101{)}_2$

যেহেতু, 01010101 ঋণাত্মক। সুতরাং 01010101 এর ২-এর পরিপূরক করতে হবে।

$\because (-01010101{)}_2=(10101011{)}_2$

সুতরাং, ইংরেজি ও আইসিটি বিষয়ে প্রাপ্ত নম্বরের পার্থক্য,

$=(01011001{)}_2+(-01010101)$

$=(01011001{)}_2+(10101011{)}_2$

ক্যারি বিট বিবেচনা করা হয় না। সুতরাং, ইংরেজি ও আইসিটি বিষয়ে প্রাপ্ত নম্বরের পার্থক্য $(00000100{)}_2$, বা দশমিক $(4{)}_{10}$।

 Sylhet Board ICT 2024 Question and Solution

ক. EBCDIC কী?
খ. 3+3+3=11 কীভাবে সম্ভব? ব্যাখ্যা করো।
গ. চিত্র-২ কে কী ধরনের গেইট বলা হয়? ব্যাখ্যা করো।
ঘ. শুধু চিত্র-১ এর গেইট দ্বারা চিত্র-৩ এর গেইট বাস্তবায়ন সম্ভব কী? তোমার উত্তরের সপক্ষে যুক্তি দাও।

$ক$

EBCDIC হলো- Extended Binary Coded Decimal Information Code এর সংক্ষিপ্ত রূপ যেটিকে মূলত আলফানিউমেরিক কোড বলা হয়।

$খ$

দশমিক সংখ্যা পদ্ধতিতে 3 + 3 + 3 = 9 হয়। কিন্তু দশমিক 9-কে অক্টালে পরিণত করলে পাই,

$\therefore (9{)}_{10}=(11{)}_8$

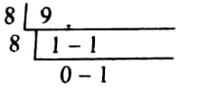
সুতরাং অক্টাল সংখ্যা পদ্ধতিতে 3+3+3 = 11 হয়।

$গ$

জেলার উদ্দীপকের চিত্র-২ হলো নর গেইট। নর গেইট একটি সর্বজনীন গেইট। যে সকল গেইট দ্বারা মৌলিক গেইটসহ অন্যান্য সকল গেইটসমূহকে তৈরি বা বাস্তবায়ন করা যায় সেই সব গেইটকে সর্বজনীন গেইট বলে। নর গেইটের মাধ্যমে যদি OR, AND এবং NOT গেইট সর্বজনীন গেইট হিসেবে প্রতিষ্ঠা পাবে। নিম্নে তা বাস্তবায়ন করে দেখানো হলো-

নর গেইট দিয়ে মৌলিক গেইট বাস্তবায়ন নিম্নে দেখানো হলো-

নট গেইট:

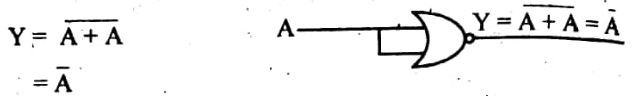
ফলে নর গেইটটি একটি নট গেইট হিসেবে কাজ করে।

অর গেইট:

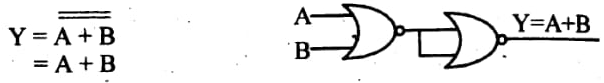
অ্যান্ড গেইট:

$ঘ$

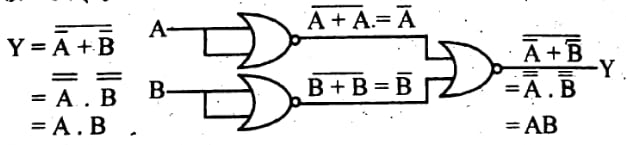
উদ্দীপকে উল্লিখিত চিত্র-১ হলো ন্যান্ড গেইট এবং চিত্র-৩ হলো এক্স-নর গেইট। ন্যান্ড গেইট ব্যবহার করে এক্স-নর গেইট বাস্তবায়ন নিম্নে দেখানো হলো:

A ও B দুটি চলকের জন্য XOR গেইটের সমীকরণ-

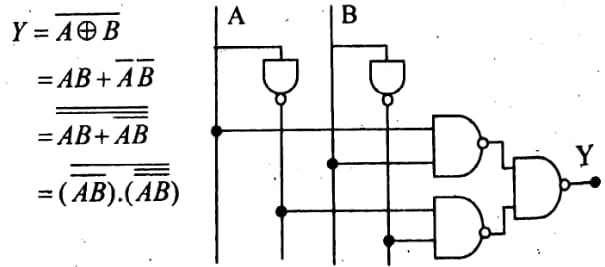
সুতরাং উপরোক্ত আলোচনা হতে বলা যায় যে, ন্যান্ড গেইট দ্বারা এক্স- নর গেইট বাস্তবায়ন সম্ভব।

Path Abdur Rahman Prince, পাঠ আব্দুর রহমান প্রিন্স, Sylhet Board ICT 2024, HSC ICT Chapter 3, Number System Solutions, Logic Gate Questions, HSC ICT Question Solve 2024, ICT Logic Gate Simplification, ICT সরলীকরণ, HSC ICT Sylhet Board, ICT Previous Year Questions